sábado, 29 de febrero de 2020
PROYECTO DE 4TO SISTEMA DE ECUACIONES
TRABAJO PARA ENTREGAR DE SISTEMA DE ECUACIONES 2X2
* GRÁFICO
* SUMA Y RESTA
* IGUALACIÓN
* DETERMINANTES
FECHA DE ENTREGA: 17 DE MARZO DE 2020
VALOR: 10% DE CALIFICACIÓN
ENTREGAR A MANO
SE REVISARÁ PROCEDIMIENTO Y OPERACIONES
TODOS LOS MÉTODOS LLEVARÁN COMPROBACIÓN
sábado, 22 de febrero de 2020
VÍDEOS DE MÉTODO GRÁFICO
INSTRUCCIONES: VER LOS VÍDEOS Y REALIZAR LOS EJERCICIOS EN EL CUADERNO SE CONTARÁ COMO TAREA.
ES TEMA DE EXAMEN PARA EL CUARTO PERIODO.
TEMA DE EXAMEN: MÉTODO GRÁFICO
TEMA DE EXAMEN PARA EL CUARTO PERIODO: MÉTODO GRÁFICO
Como es de esperar, el método gráfico consiste en representar las gráficas asociadas a las ecuaciones del sistema para deducir su solución. La solución del sistema es el punto de intersección entre las gráficas. La razón de ello es que las coordenadas de dicho punto cumplen ambas ecuaciones y, por tanto, es la solución del sistema.
Como vamos a trabajar con sistemas de dos ecuaciones lineales con dos incógnitas (x e y), la gráfica de cada ecuación es una recta. Como consecuencia, la intersección de las gráficas es un único punto (a, b) y la solución del sistema es x = a e y = b. No obstante, si las rectas son paralelas (no se cortan), el sistema no tiene solución, y si son iguales hay infinitas soluciones. Para poder aplicar el método gráfico debemos saber representar las gráficas de las rectas. Nosotros lo haremos uniendo puntos calculados previamente.
Ejemplo:
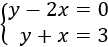
Resolución:
Lo primero que hacemos es despejar la y en ambas ecuaciones.
Primera ecuación:
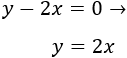
Segunda ecuación:
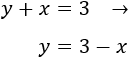
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Utilizamos, por ejemplo, x = 0 y x = 2.
Para la primera función tenemos la tabla
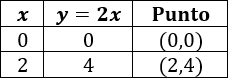
Para la segunda función tenemos la tabla (utilizando los mismos valores para x):
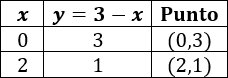
Representamos los puntos de las tablas y los unimos:
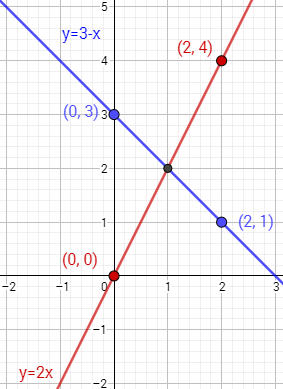
La solución del sistema es el punto donde las gráficas se cortan:
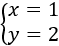
sábado, 8 de febrero de 2020
SISTEMA DE ECUACIONES (SUMA - RESTA)


MÉTODOS DE SUMA Y RESTA
Método de eliminación por suma o resta
Los siguientes pasos nos facilitan la aplicación del método:
a) Se multiplican los miembros de una o de las dos ecuaciones por una cantidad constante
apropiada para obtener ecuaciones equivalentes que tengan igual coeficiente para una de las
incógnitas.
b) Por suma o resta se elimina una de las incógnitas.
e) Se resuelve la ecuación lineal resultante.
f) Se sustituye el valor determinado en cualquiera de las ecuaciones originales para,
encontrar el valor de la otra incógnita.
Si las ecuaciones del sistema tienen alguna de las incógnitas de igual coeficientes el paso
primero se omite. EJEMPLO:
1. Resolver el sistema
(1) 4x + 6y = -3
(2) 5x + 7y = -2
Multiplicar los miembros de la ecuación (1) por 5 y los de la ecuación (2) por -4; resultando que los coeficientes de "x" se igualan y son de signo contrario.
5(4x + 6y = -3) 20x + 30y = - 15
-4(5x + 7y = -2) -20x - 28y = 8
Sumando algebraicamente ambas ecuaciones, resulta:
20x + 30y = - 15
- 20x - 28y = 8
0 2y = - 7
Resolviendo la ecuación, tenemos: y = - 7/2
Sustituyendo el valor determinado en cualquiera de las ecuaciones originales, se obtiene:
(1) 4x + 6(-7/2) = - 3
4x - 21 = - 3
4x = - 3 + 21
x = 18 / 4
x = 9/2
(2) 5(9/2) + 7(-7/2) = - 2
45/2 - 49/2 = -
-4/2 = -2
-2 = -2
Su comprobación es:
4(9/2) + 6(-7/2) = - 3
18-21 = -3
-3 = -3
Por lo tanto los valores que satisfacen al sistema son:
x = 9/2 y y = -7/2
MÉTODO DE Sustitución
El método de sustitución consiste en despejar en una de las ecuaciones cualquier incógnita,
preferiblemente la que tenga menor coeficiente, para, a continuación, sustituirla en otra
ecuación por su valor.
En caso de sistemas con más de dos incógnitas, la seleccionada debe ser sustituida por su valor
equivalente en todas las ecuaciones excepto en la que la hemos despejado. En ese instante,
tendremos un sistema con una ecuación y una incógnita menos que el inicial, en el que podemos
seguir aplicando este método reiteradamente. Por ejemplo, supongamos que queremos resolver por sustitución este sistema:
En la primera ecuación, seleccionamos la incógnita
posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
El siguiente paso será sustituir cada ocurrencia de la incógnita
obtener una ecuación donde la única incógnita sea la
Al resolver la ecuación obtenemos el resultado
por su valor en alguna de las ecuaciones originales obtendremos
queda ya resuelto.
  |
Suscribirse a:
Comentarios (Atom)
-
TEMA: INECUACIONES DE PRIMER GRADO CON DOS VARIABLES OBJETIVO: El alumno debe desarrollar habilidades de razonamiento lógico, abstra...
-
¡BUEN DÍA! ALUMNOS DEL 4010 FAVOR DE DESCARGAR CRONOGRAMA DE ACTIVIDADES DE LA MATERIA DE MATEMÁTICAS IV "ÁLGEBRA" ¡DESC...

